


|
| 1 Horror Vacui 2 A Very Patient Turtle Who Draws Lines 3 A Taxonomy of Fractology 4 Gallery of Specimens |
| Root 2 Family | Root 3 Family | Root 4 Square Grid Family | Root 4 Triangle Grid Family |
| Root 5 Family | No Root 6! | Root 7 Family | Root 8 Family |
| Root 9 Square Grid Family | Root 9 Triangle Grid Family | Root 10 Family | Root 12 Family |
| Root 13 Square Grid Family | Root 13 Triangle Grid Family | Root 16 Square Grid Family | Root 16 Triangle Grid Family |
| Root 17 and Beyond... | 5 My Brain Fillith Over | 6 References | 7 Acknowledgements |


|
| We are about to explore one of the most versatile, fertile, and abundant families of plane-filling fractal curves: the root9 triangle grid family. The first specimen to mention is none other than...the Koch Curve! Yes, our old friend Koch lives in a triangular grid, and its interval length is 3 units long. The Koch curve has many cousins, and you'll see some similarities. |

|
| What happens if you draw the first three segments of the Koch Curve and then instead of heading straight to the end, you flip back and draw the remainder as a reflected Koch? Well, here's what you get. |

|

|
|
With this curve, which I call "Reflected Koch", the fractal dimension goes up to ~1.77, since it has 7 segments instead of 4. Below is a table showing these two curves, and one other member of the root9 triangle grid family. You can see that the reflected Koch has obvious similarities to the Koch Curve, having the same profile reflected on top and on the bottom. The curve shown at the bottom does not have the same profile: its generator has a triangle balanced upside-down on top of the Koch bump: it fractalizes upward to make a triangle-shaped conifer tree with a lovely Koch Snowflake inside (shown at right). I call it "Koch Holiday Tree".
|

|

|
| Now, taking the Koch Holiday Tree generator, let's add a triangular bump at the left, and try a few variations in flippings. Here are two results: |

|
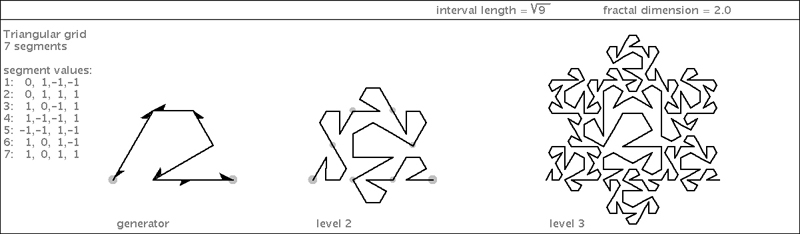
| Notice that the fractal dimension has gone up to ~1.89. It seems we are getting close to filling a triangle, but there are still holes. One more variation, with some clever flippings brings the total number of segments to 9. Tada - we have a plane-filling curve! |

|
| This is shown in higher resolution with rounded corners and filled-in, on the next page. |

|
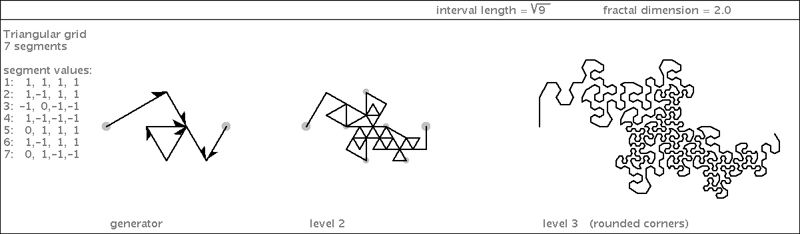
| Can a generator with fewer than 9-segment be used to fill a triangle? Sure thing. But at least one segment has to be longer than 1. This next specimen has a generator with 6 segments, and one of those segments has a length of root3. I call it "Sawtooth". As you would expect, the process by which the triangle gets filled is less regular than with the last specimen. |

|

|
| This specimen cannot plane-fill the triangle: its dimension is only ~1.77. |

|
| This specimen is a plane-filler. It is a relative of the Koch Holiday Tree I showed you earlier. I call it "Plane-filler Holiday Tree". Strangely enough, this one fills the triangle but it also dips down into the soil - perhaps to nourish its leaves. |
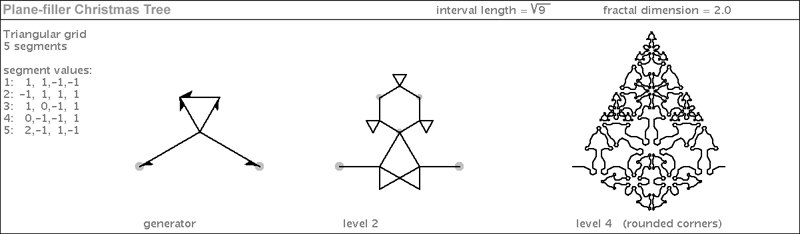
|

|
| This one is related to the plane-filler Holiday tree. It has a stylish asymmetric flair. |
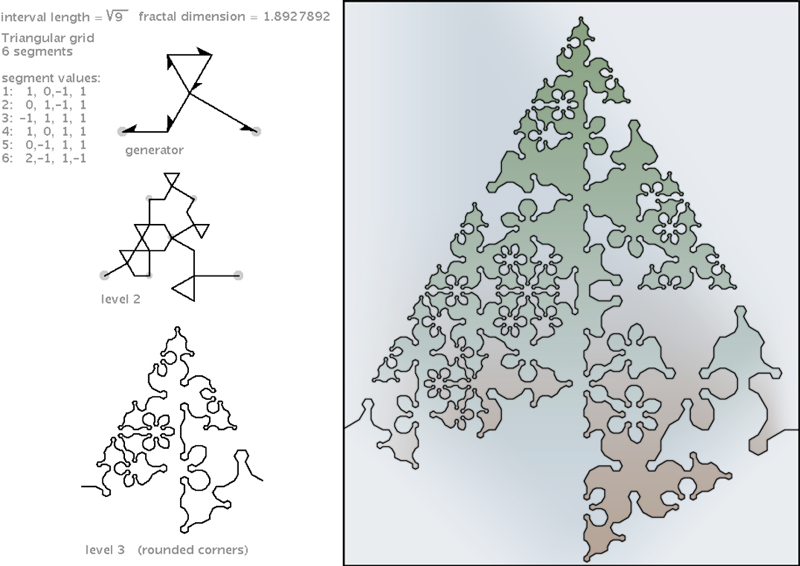
|

|
| Here's what happens if we use the same generator shape and fiddle with the flippings: |
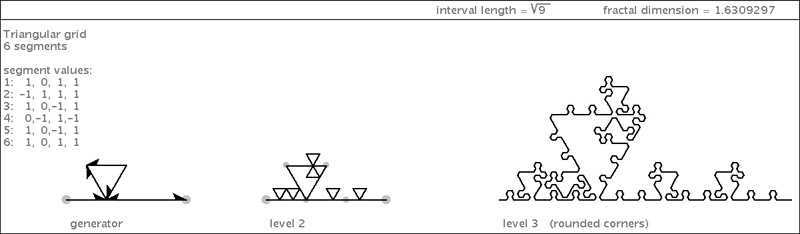
|
| Now, if we make a reflection of this triangle underneath the horizontal line, and use no flippings, we have a gridfiller! |

|
| And, what if we shift that lower triangle to the right? Here's what we get: |

|
|
Did you notice something? This has the same shape as the pinched Ter-Dragon of the root3 family we met earlier. You can see that this generator is made up of three copies of the Ter-Dragon, but they are not arranged in the usual Ter-Dragon way.
Now check out this variation of the specimen, shown below. It is rendered with splines on the next page. |

|

|
| The root9 triangle grid family includes one of the finest specimens of all: the Snowflake Sweep, featured in Mandelbrot's book: |
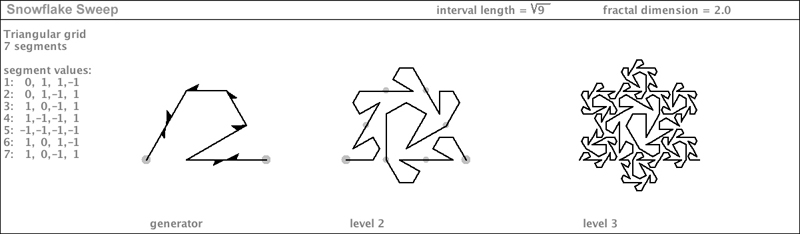
|

|
|
Notice how it fills the Koch snowflake.
Earlier I pointed out that Mandelbrot had said he "designed" a self-avoiding curve; I suggested that the curve could just as easily have been "discovered". Well, Mandelbrot's Snowflake Sweep is so amazing and beautiful that I can hardly blame him for claiming to be its designer. By the way, this curve is very flexible. Any segment in the generator can have an arbitrary flipping in its x value, and the teragons will still be self-avoiding. On the next page is a variation in x-flippings. |
|
|
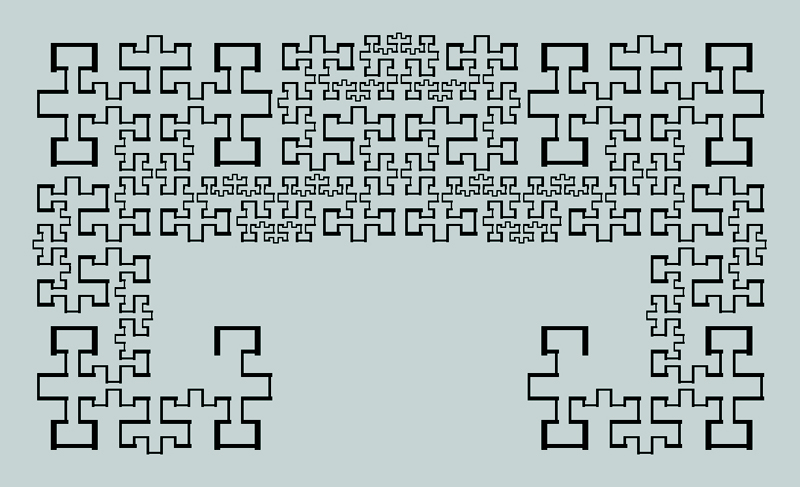
Root9 Carpets
Now I want to show you a series of root9 triangle grid family curves that incorporate segments of length root3, and fractalize to fill a tilted rectangle. I call them "root9 Carpets". I have uncovered several of them. Here is a small selection, for your brain-filling pleasure. In all cases, the 4th or 5th teragons are shown with rounded corners. |

|

|

|

|

|

|

|
|
Unraveled Carpets
I showed you the following curve early on in the book. This curve seems to be related to the carpets series, except that the weaving has come undone. I call it "Unraveled Carpet". |

|
| Here's a variation on the same generator that makes another unraveled carpet. This one seems a bit more orderly in its unraveling. |

|
| The specimen on the next page has unraveled itself in a strange way - and it is also a self-crosser. |

|

|
|
Where Be Dragons?
Are there any dragons in this family? In fact there is a whole clan of them. This clan of dragons consist of complexified 3x-scaled variations of a root3 specimen we met early on in the book - shown at left. I found three, but I have a suspicion that there are many more hiding in the deep root9 sea. |

|
| Each generator in this clan of dragons has five segments. Two of those segments have a length of root3, and the remaining three segments are of length 1. As I showed you earlier, squaring each of these lengths and then adding them results in a number that determines the fractal dimension. In this case, we get 9. On the next page is a color rendering of the self-avoiding curve below. And then I'll show you two others in the clan. |

|

|

|

|

|
| This specimen resolves to the same shape as the orderly unraveled carpet I just showed you. |

|
| This next curve is a self-avoider. On the next page I show it in color with rounded corners, on a triangle initiator. |

|

|
| These two self-avoiders, based on the same generator, are quite similar, but look closely: you can see subtle differences. |

|
| Here's another self-avoider. I call it "Brainfolds". (It was drawn by the turtle early on in the book). |

|
| I had assumed that Brainfolds would fractalize to the same shape as the specimen at the upper-left of this page. My estimation was not quite right: there seems to be at least one small difference, shown at right: The pink region is a mirror image of the green region indicated by the arrow. |

|
| This next curve resolves to a 3x-size Ter-Dragon. Notice that the first segment in the generator has a length of root3, and that the rest of the generator consists of two Ter-Dragon generator-like shapes. |
|

|
| Here is a curve whose horizontal segments have length 1 and whose vertical segments have length root3. Even though it lives in the triangular grid, it has 90-degree angles. But that doesn't qualify it as a member of the square grid family! And check it out - this is a natural self-avoider. |

|
|
| Here are a few rather zig-zaggy specimens: one is a busy dragon-like gridfiller and the other has a dimension of ~1.77. |

|
| The remaining specimens of this family that I will show you have dimension ~1.89. |

|

|
| I call this one "Dolphins" |

|

|
| These last two curves are true gems. They are both based on the same generator shape. |

|

|

|
| End of chapter. |

|
| 1 Horror Vacui 2 A Very Patient Turtle Who Draws Lines 3 A Taxonomy of Fractology 4 Gallery of Specimens |
| Root 2 Family | Root 3 Family | Root 4 Square Grid Family | Root 4 Triangle Grid Family |
| Root 5 Family | No Root 6! | Root 7 Family | Root 8 Family |
| Root 9 Square Grid Family | Root 9 Triangle Grid Family | Root 10 Family | Root 12 Family |
| Root 13 Square Grid Family | Root 13 Triangle Grid Family | Root 16 Square Grid Family | Root 16 Triangle Grid Family |
| Root 17 and Beyond... | 5 My Brain Fillith Over | 6 References | 7 Acknowledgements |


|
Brain-filling Curves - A Fractal Bestiary
by Jeffrey Ventrella Distributed by Lulu.com Cover Design by Jeffrey Ventrella |
Book web site:
BrainFillingCurves.com
ISBN 978-0-9830546-2-7 Copyright © 2012 by Jeffrey Ventrella |

eyebrainbooks.com |

FractalCurves.com |