


|
| 1 Horror Vacui 2 A Very Patient Turtle Who Draws Lines 3 A Taxonomy of Fractology 4 Gallery of Specimens |
| Root 2 Family | Root 3 Family | Root 4 Square Grid Family | Root 4 Triangle Grid Family |
| Root 5 Family | No Root 6! | Root 7 Family | Root 8 Family |
| Root 9 Square Grid Family | Root 9 Triangle Grid Family | Root 10 Family | Root 12 Family |
| Root 13 Square Grid Family | Root 13 Triangle Grid Family | Root 16 Square Grid Family | Root 16 Triangle Grid Family |
| Root 17 and Beyond... | 5 My Brain Fillith Over | 6 References | 7 Acknowledgements |


|
| Now we come to the root5 family. We have already met the 5-dragon: |

|
| Remember how I flipped the x values of all the segments of the Ter-Dragon to make the Inverted Ter-Dragon? Well, the same can be done with the 5-Dragon. And, just like the inverted Ter, the inverted 5-Dragon has a pinched waist. |

|
| This next specimen is Mandelbrot's Quartet: "Each 'player', and the table between them, pertile." [16]. He claims to have "designed" it, although one could debate that such a curve is "discovered" rather than "designed". In either case, it is one of the finest self-avoiders. |

|

|
| I discovered a variation of this generator, created by reversing the x-flipping of each segment. I call it "Inner-flip Quartet". |

|
| Next I will show you six variations on a single generator shape. Two examples are shown on the next page. The first example has an interesting property: due to the flippings, the orientations of copies of the generator do not correspond with a continuous square grid. You can see this in the mixture of 90 and 45-degree angles in the level 2 teragon. I would not have expected a curve like this to survive the fractal test. There is indeed self-contacting in several vertices, but other than that, it is rather well-behaved, as indicated by rendering with rounded corners. |

|
| A close relative of this curve is shown here. |

|
| These two specimens resolve to the same general shape, as indicated by the illustration below. |

|
| Given the same generator, with alternate flippings, we get two gridfillers with very craggy boundaries: |

|
| With other changes in flippings, we get the following gridfillers: |

|
| In that last one, notice how the conifer tree-like spike at the upper-right corresponds to the empty gap at the bottom, rotated by 90 degrees. My brain is pertiling! |

|
| Here are two plane-filling curves of the root5 family that use a common generator shape. |

|

|
|
That last curve can be combined with a 180-degree flipped copy of itself to make the shape of the 5-Dragon...
|
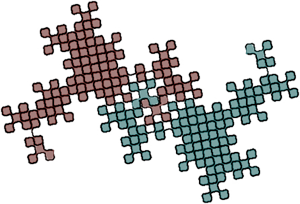
|
| This next curve is a self-avoider. It is followed by a similar specimen. |

|

|
|
Each of these last two curves can be copied four times - each copy rotated 90 degrees - and joined together to make a continuous curve. The overall shape is a replica of the Quartet (one of them is a mirror-image of the other). This appears to be a property of many root5 curves I have shown.
|

|
| End of chapter. |

|
| 1 Horror Vacui 2 A Very Patient Turtle Who Draws Lines 3 A Taxonomy of Fractology 4 Gallery of Specimens |
| Root 2 Family | Root 3 Family | Root 4 Square Grid Family | Root 4 Triangle Grid Family |
| Root 5 Family | No Root 6! | Root 7 Family | Root 8 Family |
| Root 9 Square Grid Family | Root 9 Triangle Grid Family | Root 10 Family | Root 12 Family |
| Root 13 Square Grid Family | Root 13 Triangle Grid Family | Root 16 Square Grid Family | Root 16 Triangle Grid Family |
| Root 17 and Beyond... | 5 My Brain Fillith Over | 6 References | 7 Acknowledgements |


|
Brain-filling Curves - A Fractal Bestiary
by Jeffrey Ventrella Distributed by Lulu.com Cover Design by Jeffrey Ventrella |
Book web site:
BrainFillingCurves.com
ISBN 978-0-9830546-2-7 Copyright © 2012 by Jeffrey Ventrella |

eyebrainbooks.com |

FractalCurves.com |