


|
| 1 Horror Vacui 2 A Very Patient Turtle Who Draws Lines 3 A Taxonomy of Fractology 4 Gallery of Specimens |
| Root 2 Family | Root 3 Family | Root 4 Square Grid Family | Root 4 Triangle Grid Family |
| Root 5 Family | No Root 6! | Root 7 Family | Root 8 Family |
| Root 9 Square Grid Family | Root 9 Triangle Grid Family | Root 10 Family | Root 12 Family |
| Root 13 Square Grid Family | Root 13 Triangle Grid Family | Root 16 Square Grid Family | Root 16 Triangle Grid Family |
| Root 17 and Beyond... | 5 My Brain Fillith Over | 6 References | 7 Acknowledgements |


|
| The root9 square grid family has many interesting plane-filling curves. The square root of 9 is of course 3. And, being an integer, my scheme places the interval length horizontal, stretching across three grid cells. We already encountered one member of this family early on when I showed you the Koch curve: its friend, the Square Koch. Here is its diagram: |
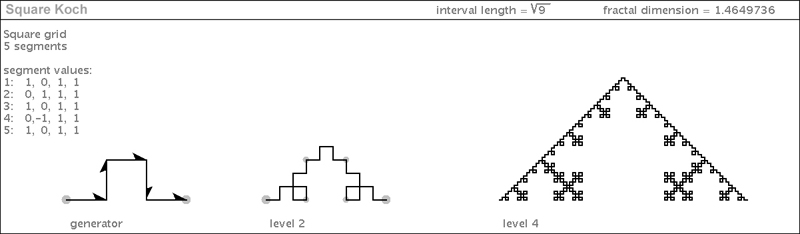
|
| Now let's add a floor and a basement to this generator and see what happens. Lo and behold, we get one of the most familiar - and oldest - plane-filling curves of all time: the "Original Peano Curve" (as Mandelbrot called it: Giuseppe Peano explored many variations). Rounded corners help a lot when viewing this curve. |
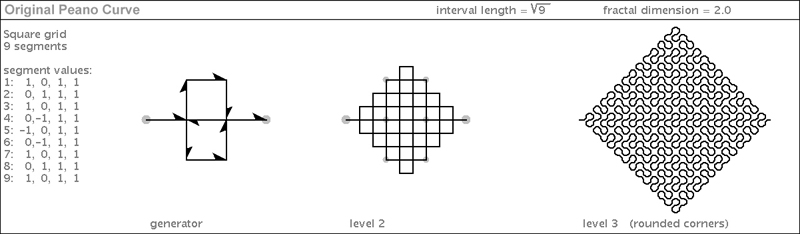
|
| Here is a variation that fills the same area as the original Peano curve, but the shape it fills is a right triangle: |
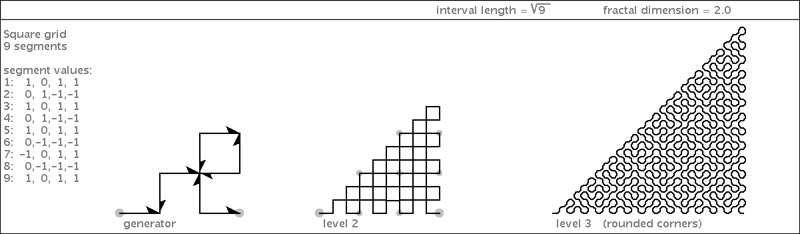
|
| And here is a familiar theme once again: a generator shape can be made to create either a right triangle or a dragon, by way of alternate flippings. This variation is like a dragon (okay, maybe it's not like a dragon... let's just go with "jaggy"). |
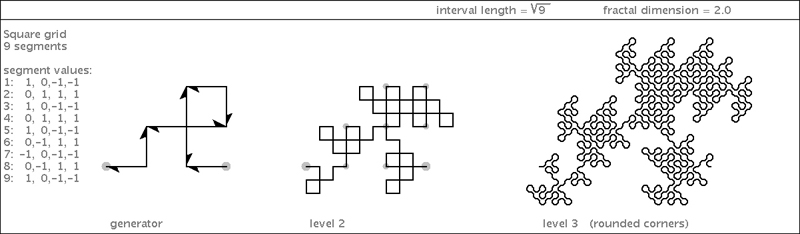
|
| Where there be dragons...there be castles. The root9 Castle below is filled with holes...holes of all sizes. It is a holey castle. No surprise: its fractal dimension is only ~1.77. |
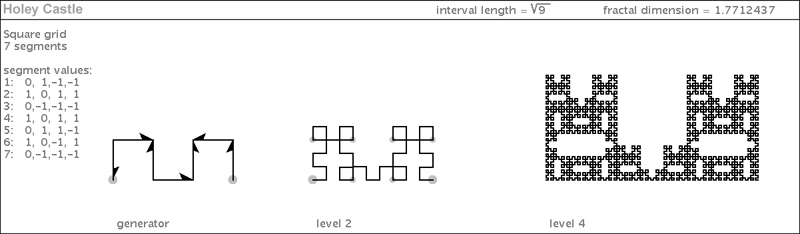
|
| The Holey Castle is related to a large class of fractals that are riddled with holes, such as the Sierpinski Triangle and the Sierpinski Carpet (and their 3D counterparts: the Tetrix and the Menger Sponge): |

|
| Remember the variation of Cesaro's Sweep I showed you from the root4 family? It has a double-sided vertical needle. Well, I wondered if there might be something similar in the root9 square grid family ...and I came up with the generator below. Like Cesaro's Sweep, this curve is everywhere edge-self-touching except for the bottom edge. But unlike Cesaro's Sweep, it has a wonderful fractal boundary. Its 4th teragon is shown below at right. Rounded corners help only slightly to reveal the curve's trajectory. |
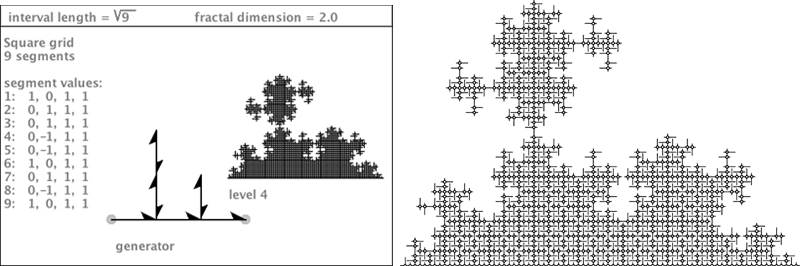
|
| Below is an intriguing fractal curve of dimension ~1.77. |
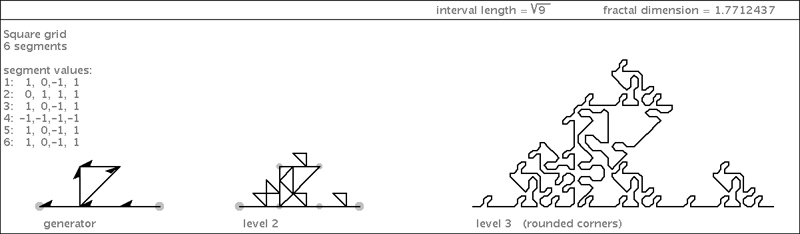
|
| Here are two gridfillers based on a common generator: |
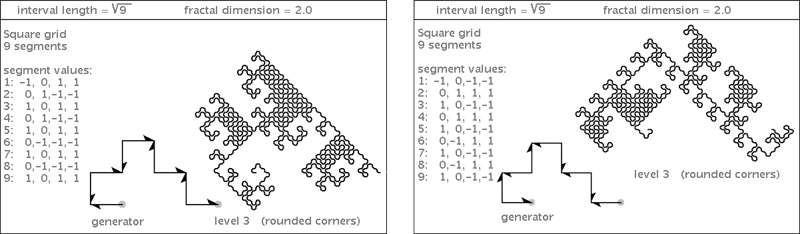
|
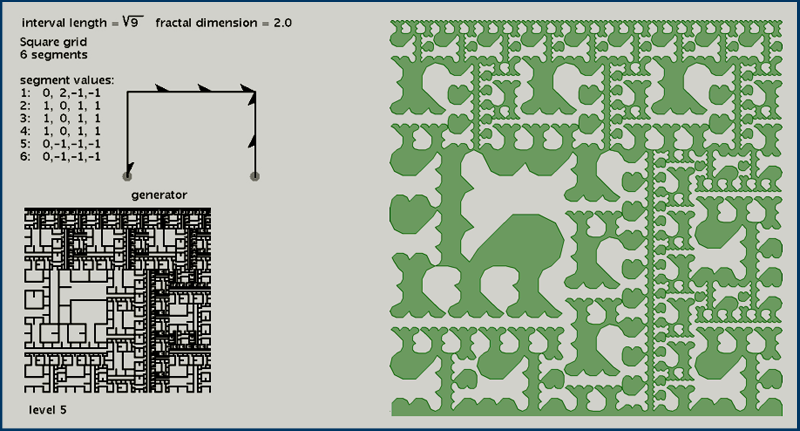
| The sepcimen below has a generator with a 2-length segment corresponding to a 2x2 square (shown in purple at right). It has a lot of self-touching edges, and so I used the low-pass smoothing filter to render level 5 with filled-in areas to show the interesting self-similarity. |
|
|
| End of chapter. |

|
| 1 Horror Vacui 2 A Very Patient Turtle Who Draws Lines 3 A Taxonomy of Fractology 4 Gallery of Specimens |
| Root 2 Family | Root 3 Family | Root 4 Square Grid Family | Root 4 Triangle Grid Family |
| Root 5 Family | No Root 6! | Root 7 Family | Root 8 Family |
| Root 9 Square Grid Family | Root 9 Triangle Grid Family | Root 10 Family | Root 12 Family |
| Root 13 Square Grid Family | Root 13 Triangle Grid Family | Root 16 Square Grid Family | Root 16 Triangle Grid Family |
| Root 17 and Beyond... | 5 My Brain Fillith Over | 6 References | 7 Acknowledgements |


|
Brain-filling Curves - A Fractal Bestiary
by Jeffrey Ventrella Distributed by Lulu.com Cover Design by Jeffrey Ventrella |
Book web site:
BrainFillingCurves.com
ISBN 978-0-9830546-2-7 Copyright © 2012 by Jeffrey Ventrella |

eyebrainbooks.com |

FractalCurves.com |