


|
| 1 Horror Vacui 2 A Very Patient Turtle Who Draws Lines 3 A Taxonomy of Fractology 4 Gallery of Specimens |
| Root 2 Family | Root 3 Family | Root 4 Square Grid Family | Root 4 Triangle Grid Family |
| Root 5 Family | No Root 6! | Root 7 Family | Root 8 Family |
| Root 9 Square Grid Family | Root 9 Triangle Grid Family | Root 10 Family | Root 12 Family |
| Root 13 Square Grid Family | Root 13 Triangle Grid Family | Root 16 Square Grid Family | Root 16 Triangle Grid Family |
| Root 17 and Beyond... | 5 My Brain Fillith Over | 6 References | 7 Acknowledgements |


|
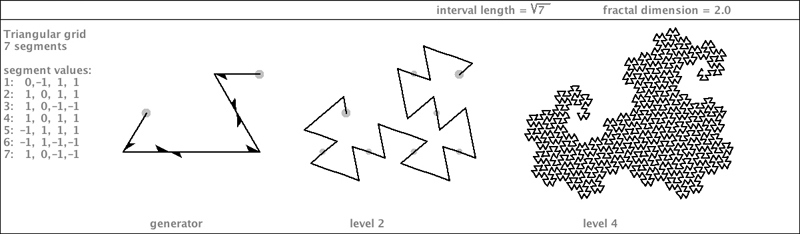
| Now we can add a new specimen to the Ter Dragon and the 5-Dragon to make a nice neat trio of prime number palindrome dragons. It is the 7-Dragon. These three curves have a few things in common: (1) they are all palindromes; (2) they require no segment flippings; (3) they represent the first three odd numbers (other than 1); and (4) they are all gridfillers. One difference is that the 7-Dragon is rather fat compared to the other two, and it is not as rough around the edges, so it may not qualify as a true "dragon". It also cannot be converted into a pinched-waist specimen by way of flipping the x values of its generator segments. Clearly, the 7-Dragon has a bit of a weight problem. Here it is: |

|
| I found a variation on the 7-Dragon generator that traverses the same segments, only in a different order. The diagram at right reveals this difference by way of rounding the corners of the generator. This alternate 7-Dragon is shown on the next page. |

|

|
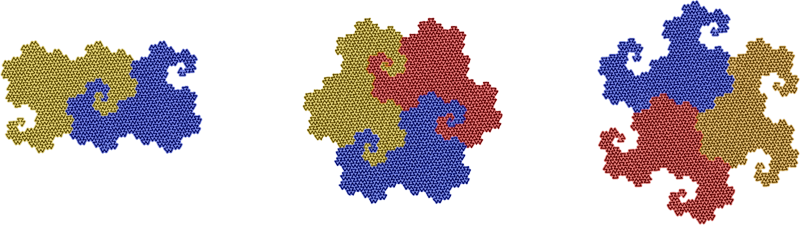
| Here is a color rendering, with rounded corners, showing how the curve is a boundary between two domains: |

|
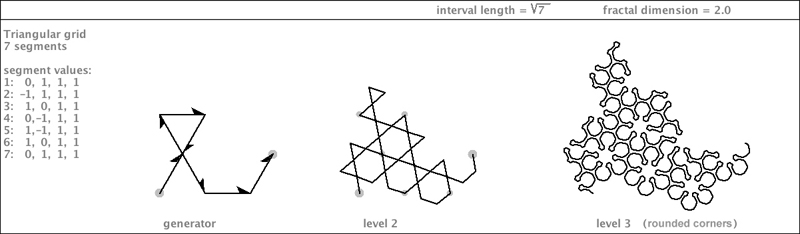
| Here is yet another variation on the 7-Dragon: |
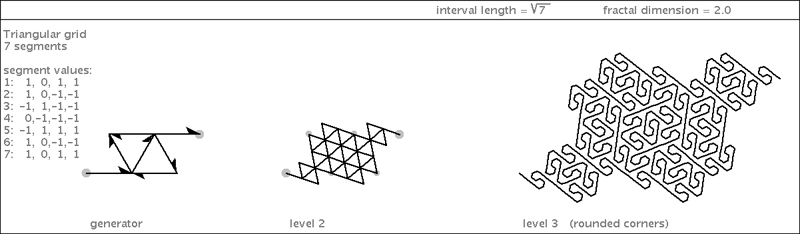
|
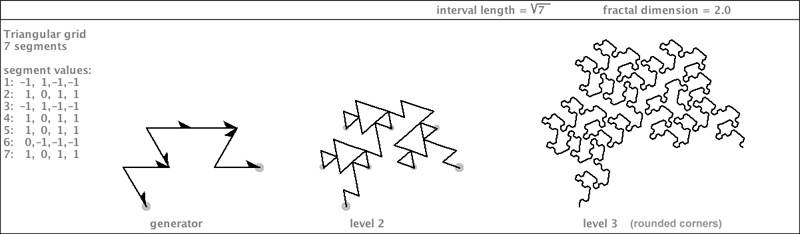
| Now, here is a strange specimen. I wouldn't normally include a self-crossing fractal curve in this book, but this variation on the 7-Dragon is irresistibly clever in it self-crossing: |
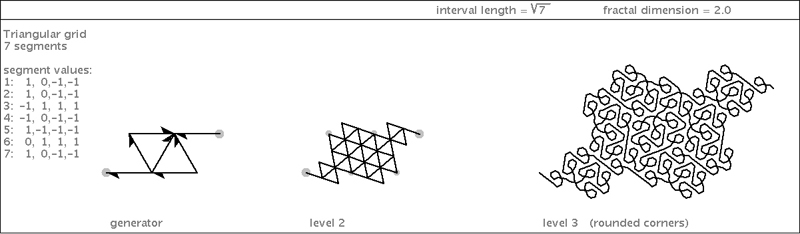
|
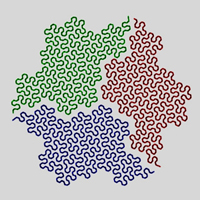
| On the next page is a diagram that shows the progression of this fractal curve. As usual for a gridfiller (or, in this case a self-crossing gridfiller) I render it with rounded corners. For this illustration, I filled-in parts of it with color, to show how regions percolate into ever-complexifying domains. |

|
|
Notice how the crossings accumulate with each level. In level 1 (upper-left) there is one crossing, which forms a closed region shown in yellow. In level 2 (upper-right) there are 7 small-loop crossings that form closed regions colored in red, and one larger-scale crossing (leftover from level 1, shown in yellow). In level 3 (bottom) there are 49 small-looped crossings that form closed off regions colored in blue. The remaining yellow and red regions have become more convoluted. I would assume that with each continuing level of fractalization, the remaining regions would stay topologically whole yet more convoluted, and that the self-similarity of clusterings would continue at each level of detail.
Now it is time to visit one of the most famous plane-filling curves of all: the Gosper Curve, a truly splendid self-avoider. |

|

|
| The Gosper curve is named after William Gosper [7]. It fills a roughly hexagonal region, which Mandelbrot called "Gosper Island". The shape of the Gosper Island will be popping up throughout our exploration of this family. Here's one example: three 7-Dragons can be combined to form a shape of the Gosper Island. |
|
|
It is a source of frustration for geometers that hexagons do not tile recursively, like squares and triangles. In other words, they are not rep-tiles. But the Gosper Curve defines a series of seven tiling regions that are all similar to the whole. So it gets around this problem...that is, if you don't mind having hexagons with craggy boundaries. |
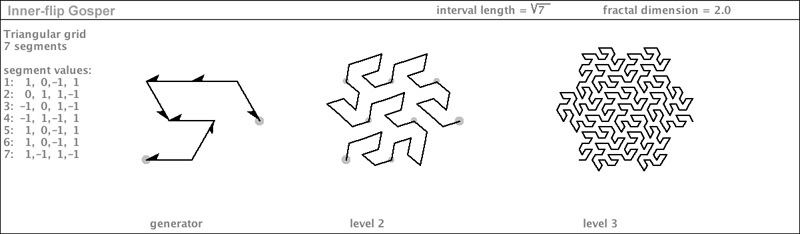
| Here is something I call the "Inner-flip Gosper". It has each of the x-values flipped, and so it creates a different character to the way the fingers curl to fill up the Gosper Island. Counting up the fractal levels, the direction of the curl reverses. |
|

|
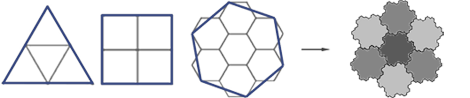
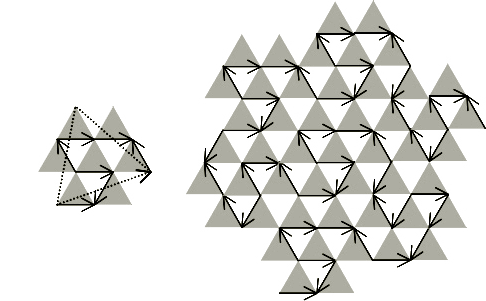
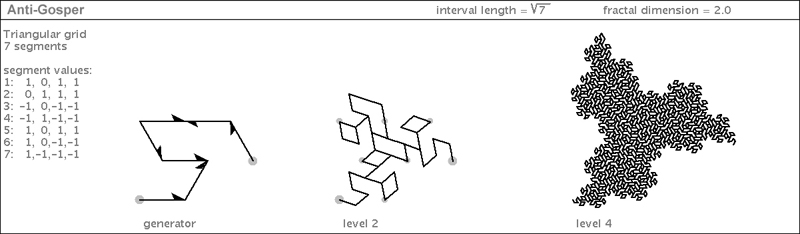
| The diagram at the right was created by Fukuda, et. al [4] to show a generalized scheme for constructing Gosper-like Curves. It can be described as a triangular checkerboard, where each gray triangle stands for a hexagonal tile. Now, keep these triangles in your mind as I show you a variation of the Gosper Curve's generator that I discovered. I call it "Anti-Gosper". Normally, the Gosper Curve is a happy self-avoiding curve. But I have seen the Gosper Curve when it is in a bad mood. When this happens, it flips three of its segments, causing its fractalized teragon to become a shriveled-up triangle. The Anti-Gosper is edge-touching, in a rather anti-social way. |
|
|
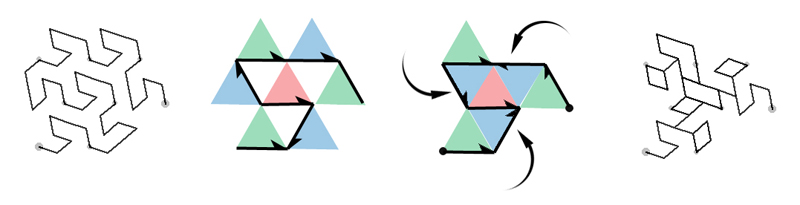
| Here is a diagram illustrating the transformation from Gosper to Anti-Gosper, where the checkerboard of triangles collapses in on itself, leaving no gaps. |
|
|
The Anti-Gosper essentially transforms the Gosper curve from a hexagon-like tiling fractal to a triangle-like tiling fractal.
The overall shape of the anti-Gosper can be created by another generator, shown here: |
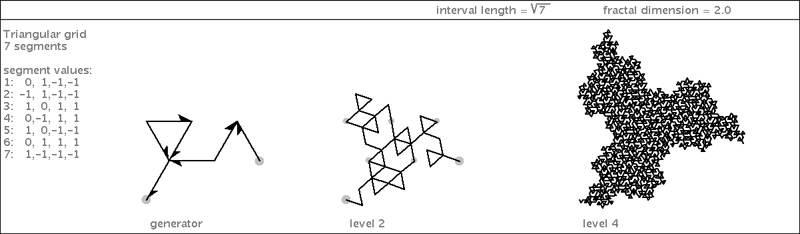
|
|
Node Gosper
Remember the node-replacement curves I showed you earlier? Well, after discovering that any fractal tiling could be used as the basis for a node-replacement curve, I realized that the Gosper curve would qualify. So here is a picture I drew of a variant of the Gosper curve, which I call "Node Gosper". Instead of the segments of the generator spanning between two corners of each hexagonal tile, they connect at midpoints of neighboring hexagonal tiles. Just for fun, I did a drawing of the second teragon of a node Gosper, and rendered the connective tissue with pink lines. Did you notice that fractal curves generated with node replacement are not strictly self-similar? The extra connective lines create slight differences in the internal shapes. In this example you can see the slight variations among the bumps. These variations accumulate progressively with each teragon. 
|
| The root7 family is genetically imbued with a talent for clever self-crossing. Here is another variation of a self-crossing dragon, followed by a colorful self-crossing Gosper Island made by combining three copies. |
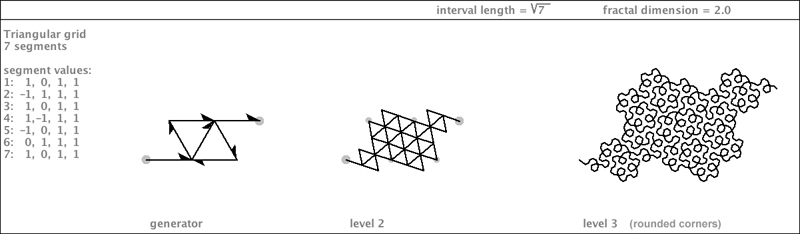
|
| Here is a root7 gridfiller, with a distinctive hook. It looks a bit like the Yin Dragon I showed you earlier of the root3 family. Below is a rendering, pertiled with a 180-degree flipped partner. The two mate to create a yin-yang 7-dragon: |
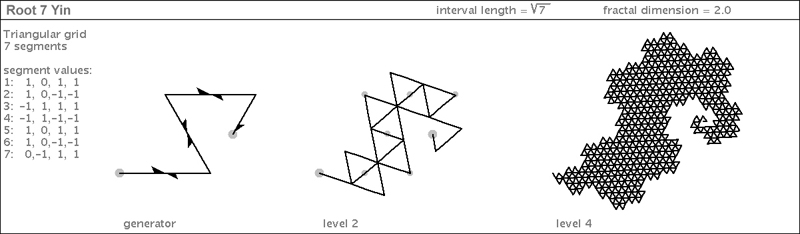
|

|
| The profile of the 7-Dragon is similar to that of the Gosper Island - that is: the fat middle-section. As I mentioned before, the Gosper Island seems to pop up quite a bit in this family. Here is a curve that shows a bit of that profile (but only in certain parts). |
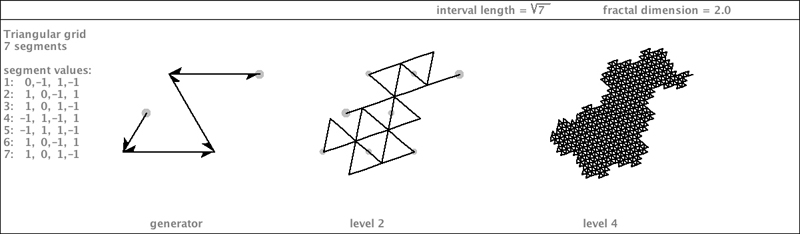
|
| Here is a curious specimen. The main part of its body looks like a Gosper Island, but it is partly-eroded. And right below the eroded part is a 7-Dragon - tethered to its body. |
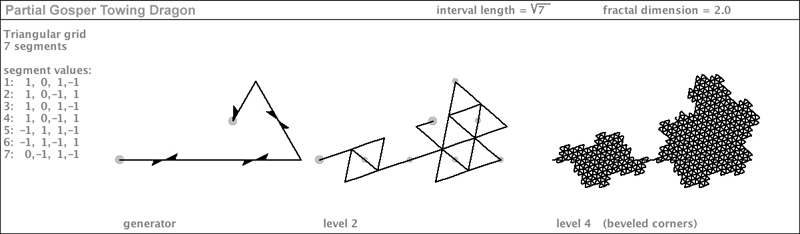
|
| I discovered a variation of the specimen I just showed you. After careful analysis, I have concluded that this specimen had made a valiant attempt to fill up the missing piece of its Gosper body. But unfortunately, it had spent too many of its segments on its tethered 7-Dragon. And in its failed attempt to fill its Gosper body, it left a series of Gosper-like holes. |
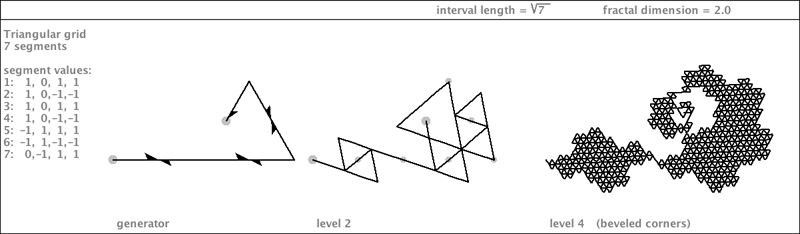
|
| Below at left is a rendering of this specimen with regions colored to illustrate the Gosper pieces. Now, do you want to see what it looks like when two of these specimens mate? It is shown below at right. Don't try to wrap your whole brain around this one - you might get a headache. |
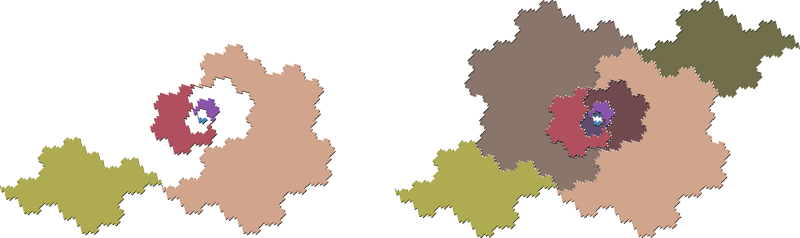
|
| The Gosper profile shows up again in these two variations on one generator. They both have a rather jaggy inner-texture. You can see in the level 2 teragon below that these shapes are still quite similar. But at level four, it becomes clear that the second specimen has two spiraling hooks. This specimen is shown below with a few rep-tiling themes. |
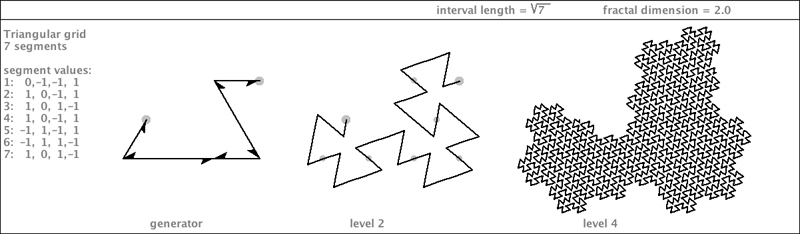
|
|
|
| Gosper profile cleverness abounds: This specimen is pertiled 6 times to form a closed Gosper Island. |
|

|
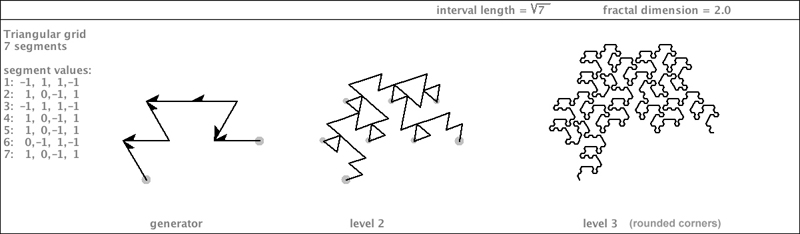
| The two specimens below create variations on a "Gosper Hill", covered with lush vegetation, shown below: |
|
|

|
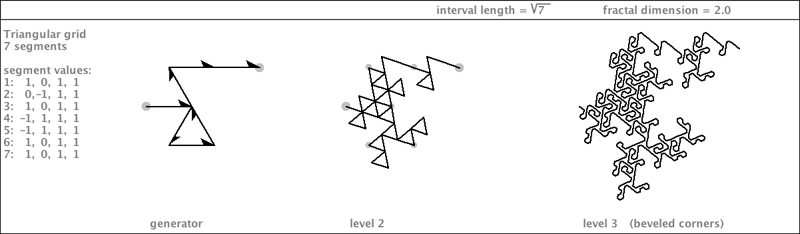
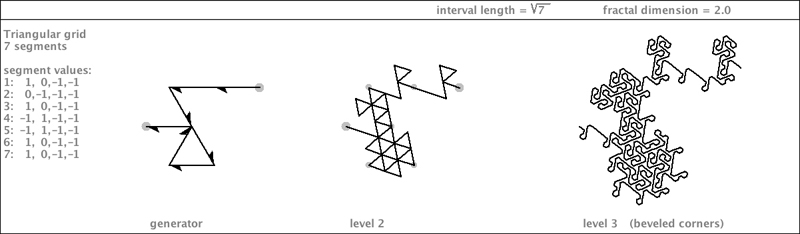
| Here are two flip-variations of a generator. They are gridfillers. The second one is shown below with an enlarged area. |
|
|

|
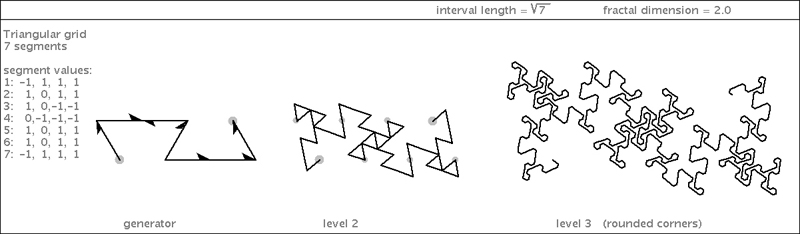
| Here are two specimens based on a common generator shape. |
|
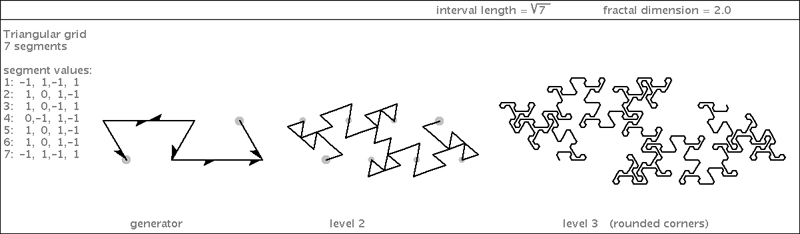
|

|
| Here is a highly craggy specimen. It is shown below in a 3-way pertiling. |
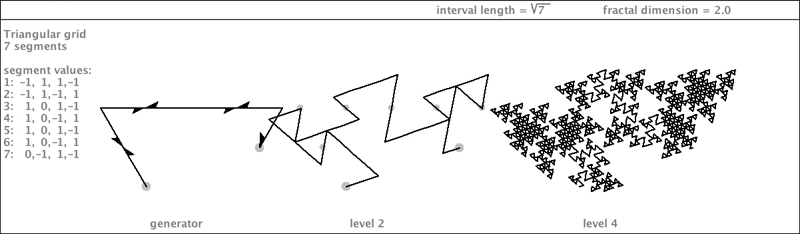
|

|
| This self-crossing curve is quite interesting. Below is a rotated rendering of teragon 4. |
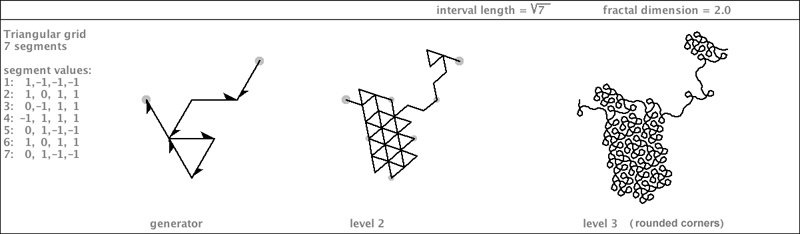
|
|
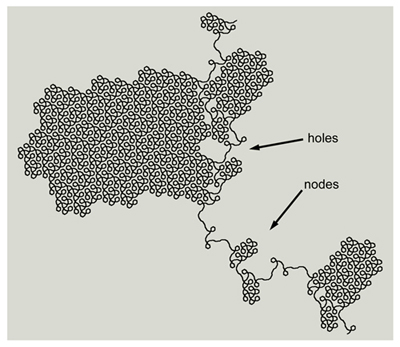
On the next page I show something about this curve that I had not initially expected. This may not come as such a surprise to you, after having seen several specimens. When I first drew this curve, I noticed that the holes in the shape corresponded to the nodes. Could it be that the nodes could fit into the holes?
So I decided to try some pertiling: I made a copy and rotated it by 120 degrees (knowing that this is a triangle-grid specimen). And lo and behold, they fit together like peas in a pod (or several peas in several pods). Then I wondered if the remaining holes might be filled by a third copy, rotated by -120 degrees. Imagine how excited I was when the three of these specimens fit together to form a Gosper Island! On the next page is a picture of this three-way mating. That's quite an intimate embrace! |

|
| End of chapter. |

|
| 1 Horror Vacui 2 A Very Patient Turtle Who Draws Lines 3 A Taxonomy of Fractology 4 Gallery of Specimens |
| Root 2 Family | Root 3 Family | Root 4 Square Grid Family | Root 4 Triangle Grid Family |
| Root 5 Family | No Root 6! | Root 7 Family | Root 8 Family |
| Root 9 Square Grid Family | Root 9 Triangle Grid Family | Root 10 Family | Root 12 Family |
| Root 13 Square Grid Family | Root 13 Triangle Grid Family | Root 16 Square Grid Family | Root 16 Triangle Grid Family |
| Root 17 and Beyond... | 5 My Brain Fillith Over | 6 References | 7 Acknowledgements |


|
Brain-filling Curves - A Fractal Bestiary
by Jeffrey Ventrella Distributed by Lulu.com Cover Design by Jeffrey Ventrella |
Book web site:
BrainFillingCurves.com
ISBN 978-0-9830546-2-7 Copyright © 2012 by Jeffrey Ventrella |

eyebrainbooks.com |

FractalCurves.com |