


|
| 1 Horror Vacui 2 A Very Patient Turtle Who Draws Lines 3 A Taxonomy of Fractology 4 Gallery of Specimens |
| Root 2 Family | Root 3 Family | Root 4 Square Grid Family | Root 4 Triangle Grid Family |
| Root 5 Family | No Root 6! | Root 7 Family | Root 8 Family |
| Root 9 Square Grid Family | Root 9 Triangle Grid Family | Root 10 Family | Root 12 Family |
| Root 13 Square Grid Family | Root 13 Triangle Grid Family | Root 16 Square Grid Family | Root 16 Triangle Grid Family |
| Root 17 and Beyond... | 5 My Brain Fillith Over | 6 References | 7 Acknowledgements |


|
| Since root4 = 2, and since square grids and triangle grids share common grid points along an axis (the horizontal "floor" of the two grids), you may suspect that there exists a family of root4 plane-filling curves that live in the triangle grid. Indeed I have discovered what I believe to be all of them. |
| But before I show you these plane-filling curves, I would first like to show you a member of the root4 triangle grid family that is not plane-filling: its fractal dimension is ~1.5849625, and it generates the famous Sierpinski Arrowhead Curve. It is identical to the Sierpinski Triangle (a solid triangle with its center triangle cut out, and then with the center triangles cut out of the remaining three, and so on)... |
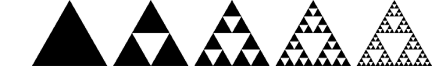
|

|
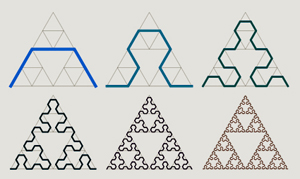
| When you fractalize the Sierpinski Arrowhead Curve, it converges toward the Sierpinski triangle. At each stage, it accumulates bays and peninsulas, which approach each other, getting closer and closer...but never touching. So in fact this is a self-avoiding curve. |
|
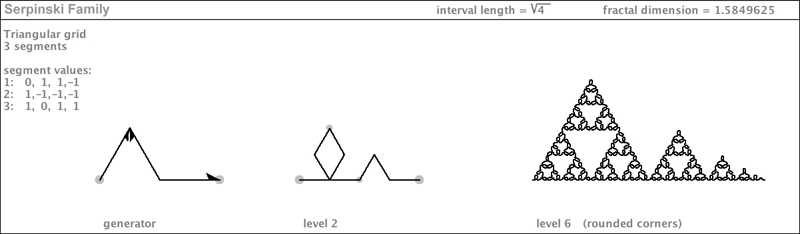
| I was delighted when I discovered a curve that actually creates a family of Sierpinski curves! In the diagram below, I show this curve fractalized to level 6. Daddy Sierpinski sits proudly to the left, with Mommy Sierpinski to his right. To her right is daughter Sierpinski, followed by little brother Sierpinski, and then baby Sierpinski, and finally, the family pet: Turtle Sierpinski. |
|
| Here is a higher-level rendering of the Sierpinski family fractal curve, with some extra members of the family to the right of the pet turtle (I leave it to you to imagine who are the tiniest members of this family). |

|
| Now it's time to look at the plane-filling members of the root4 triangle grid family. I will start with one that requires no flippings in its segments. Here it is. It happens to be a palindrome: |
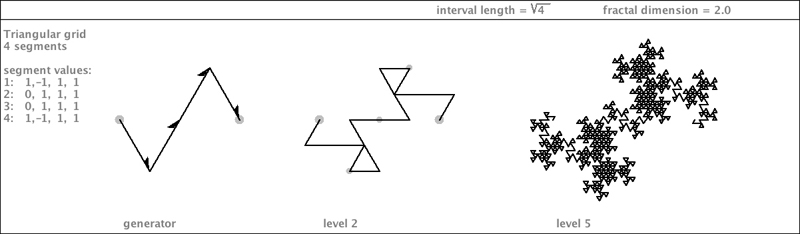
|

|
| This fractal curve is a gridfiller, but it has a wild boundary, which has a high fractal dimension of its own. Not only that: the boundary touches itself. This fractal makes the notion of "plane-filling" very fuzzy (so to speak) because the region of the plane that it fills is scattered haphazardly. All the filled-in areas of fully fractalized curves that we have seen before this one had boundaries that were either straight lines or else they were fractal curves of their own...but never self-touching. Now get ready; here is that same generator with some different flippings. Its boundary is so amazingly self-touching, you might call it "self-enveloping" (but it is NOT self-crossing, as revealed by rendering it with rounded corners). |
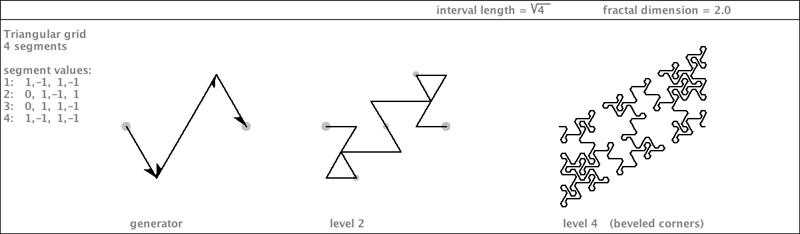
|
| When highly fractalized, this curve becomes a parallelogram filled with a cacophony of triangles. |

|
| Here is that same generator with yet another set of flippings. |
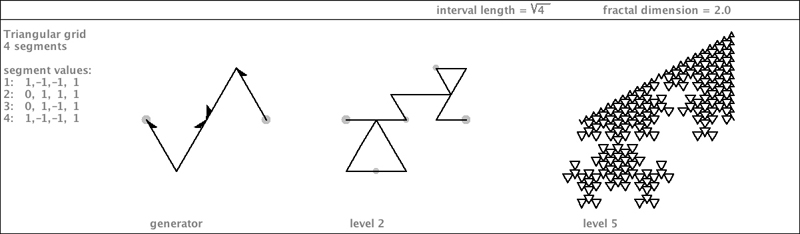
|
| Now here is a different generator of this family. This curve is highly self-enveloping. |
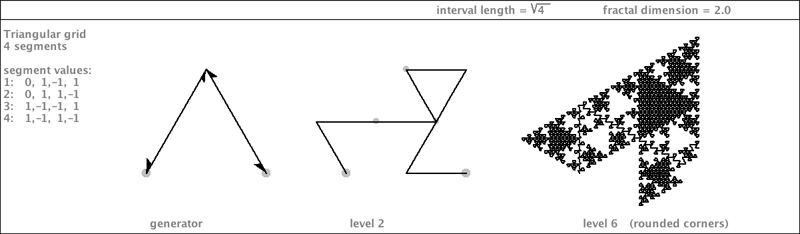
|
| On the next page is a picture showing two copies of this curve...mating. They are engaged in the most intimate embrace one can imagine. |

|
| Here is another curve based on the same generator shape. I have rendered it below with hierarchical coloring to indicate the way nodes are formed: each node has 3-way symmetry and is connected to other nodes at pinch-points. |
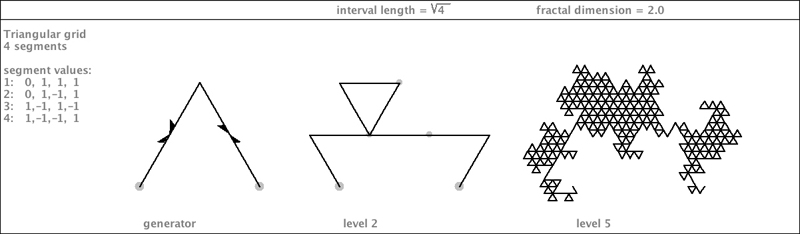
|

|
| Here is another curve based on the same generator shape. I have rendered it below with hierarchical coloring to indicate the way nodes are formed: each node has 3-way symmetry and is connected to other nodes at pinch-points. |
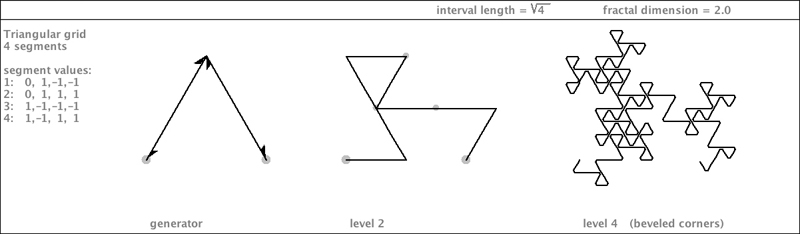
|

|
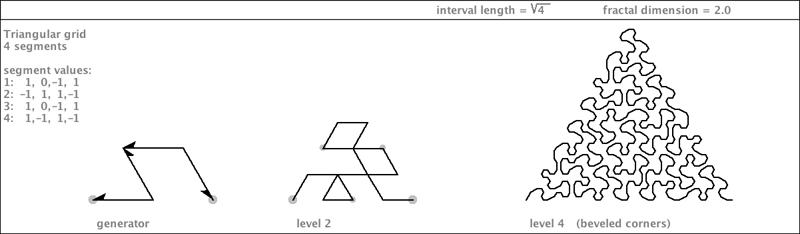
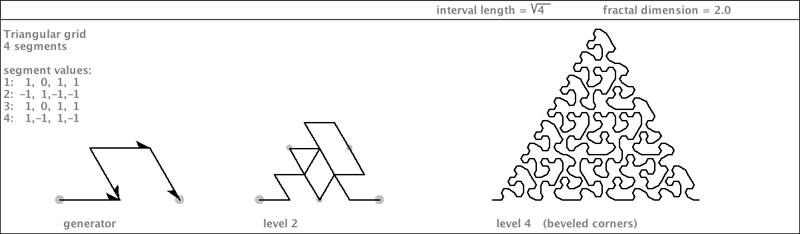
| The last members of the root4 triangle grid family I will show you are curves that exactly fill an equilateral triangle. They are pseudo-gridfillers. |
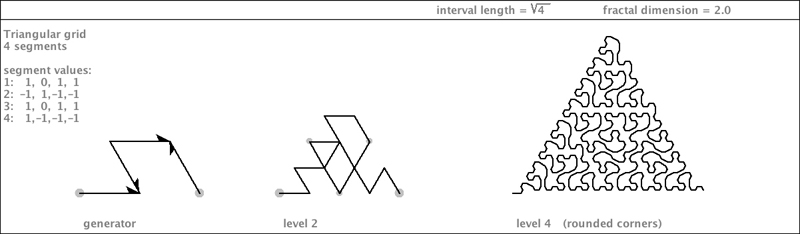
|
You can think of each of the four segments of this generator as being responsible for one of
four sub-triangles. The precise set of segment flippings is important, so as to avoid
edge-touching.
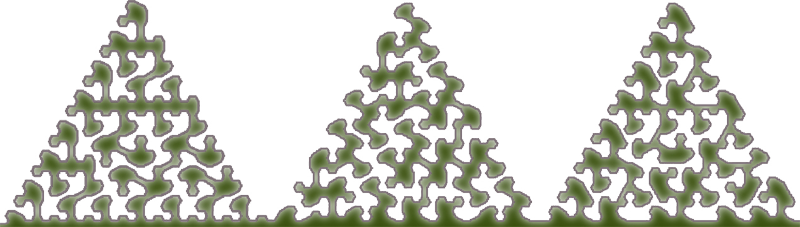
Zbigniew Fiedorowicz
[6] made a variation of this fractal - shown below.
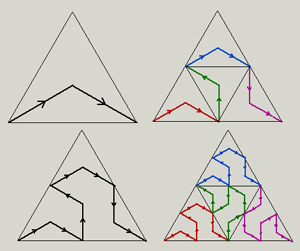
|
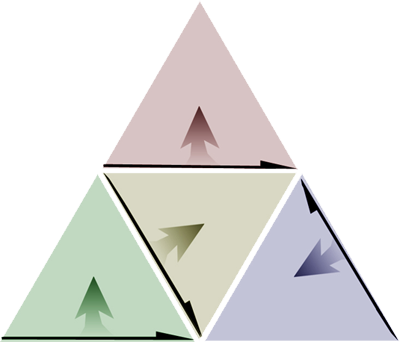
|
| Two variations are shown here, and at the bottom of the page is a portrait of all three variations at level 4. |
|
|
|
| End of chapter. |

|
| 1 Horror Vacui 2 A Very Patient Turtle Who Draws Lines 3 A Taxonomy of Fractology 4 Gallery of Specimens |
| Root 2 Family | Root 3 Family | Root 4 Square Grid Family | Root 4 Triangle Grid Family |
| Root 5 Family | No Root 6! | Root 7 Family | Root 8 Family |
| Root 9 Square Grid Family | Root 9 Triangle Grid Family | Root 10 Family | Root 12 Family |
| Root 13 Square Grid Family | Root 13 Triangle Grid Family | Root 16 Square Grid Family | Root 16 Triangle Grid Family |
| Root 17 and Beyond... | 5 My Brain Fillith Over | 6 References | 7 Acknowledgements |


|
Brain-filling Curves - A Fractal Bestiary
by Jeffrey Ventrella Distributed by Lulu.com Cover Design by Jeffrey Ventrella |
Book web site:
BrainFillingCurves.com
ISBN 978-0-9830546-2-7 Copyright © 2012 by Jeffrey Ventrella |

eyebrainbooks.com |

FractalCurves.com |