|
2. Taxonomy
We have now arrived at the core theme in this book: a taxonomy representing all plane-filling curves using edge-replacement. (For brevity, these will be referred to as “curves” throughout the book). It will be necessary to delve into some technical details and definitions before a bigger picture can take shape. You can always choose to skip ahead and study the illustrations throughout the book—to build intuition using the powers of your visual cortex. If you do, please come back to this chapter, as it presents key terms and concepts. All biological organisms are classified within a taxonomy of eight ranks: domain, kingdom, phylum, class, order, family, genus, and species. The five ranks in the taxonomy of fractal curves described in this book are not related to the taxonomy of biological organisms. However, it is intentional that the fractal curve ranks are ordered from the most general to the most specific: 1. Domain (square (Gaussian) or triangular (Eisenstein) lattice) 2. Root (the origin of a series of families) 3. Family (a class of curves based on the root) 4. Generator (the seed for generating a curve in a family) 5. Transforms (rotations and reflections applied to the generator) The hierarchy of these ranks is shown in a cartoon schematic in Figure 2.1. 
Figure 2.1. A cartoon schematic showing the hierarchy of fractal curve ranks 1. Domain Complex numbers have two parts: real and imaginary. The entire set of complex numbers fills the complex plane. It maps to a Cartesian grid, and it is infinitely dense. A subset of the complex plane—the Gaussian integers—forms a square lattice: a regular grid of points arranged orthogonally. A Gaussian integer is defined as a complex number whose real and imaginary parts are both integers. The sum, difference, or product of any two Gaussian integers is always another Gaussian integer: thus, the Gaussian integers are closed under addition and multiplication. In this book we will also include the Eisenstein integers in our definition of “complex integer”; the Eisenstein integers form a triangular lattice (explained later). They are also closed under addition and multiplication. The Gaussian and Eisenstein integers both form Euclidean domains: the fundamental theorem of arithmetic can be applied. The taxonomy described in this book is based on these two Euclidean domains. Figure 2.2 shows the Gaussian domain (G), which forms a square lattice, and the Eisenstein domain (E), which forms a triangular lattice (sometimes it is called a “hexagonal lattice”, referring to the lattice points as the centers of hexagons). 
Figure 2.2. Gaussian and Eisenstein integer lattices When we talk about integers, we are usually referring to the rational integers: those familiar evenly-spaced points that lie on the one-dimensional real number line. The complex integers occupy the plane, and thus have more geometric symmetry than the rational integers. Throughout this book, the word “integer” will typically be used in reference to complex integers. Transform to Eisenstein Complex numbers are normally expressed in the form a+bi, where a is the real part and b is the imaginary part (i denotes imaginary). Since Eisenstein integers do not line up orthogonally, they require extra specification, and are typically expressed in the form a+bω, where a and b are integers, and ω = (-1+i√3)/2. Think of this as a mapping from the square lattice to the triangular lattice. To illustrate this, Figure 2.3 shows a mapping from a unique Gaussian integer G(2,1) to a unique Eisenstein integer E(2,1). It is shifted leftward and downward, while the other integers are unchanged because they lie on the real axis. 
Figure 2.3. Mapping of integer (2,1) from Gaussian to Eisenstein The shift to these components (a, b) can be expressed as follows: a-shifted = a - b/2; b-shifted = b * √3/2. Abbreviated Notation In this book, complex integers are expressed using the simplified form (a,b)—a notation typically used to specify Cartesian coordinates. It is made explicit when the domain is Gaussian vs. Eisenstein. For instance, “E(2,5)” specifies the Eisenstein integer 2+5ω, and “G(-2, -1)” specifies the Gaussian integer -2-1i. Norm The distance of a complex number from the origin (0,0) can be calculated using the Pythagorean theorem. This is called the “Euclidian distance.” Squaring that number results in what is called the “norm.” For complex integers, the norm is always a positive rational integer. (The term “norm” is sometimes used to refer to the Euclidean distance, but that will not be used in this context).
Slices The Gaussian Integer lattice can be divided into eight pie slices (octants) that are equal except for the isometric transformations of rotation and reflection. Similarly, the Eisenstein Integer lattice can be divided into twelve slices (Figure 2.4). Given this isometry, we can ignore all but one slice for the purposes of this taxonomy; we will only refer to the slice that lies above and adjacent to the positive real axis (shown as gray in the figure). These slices will be referenced often throughout the book. 
Figure 2.4. Referenced slices of the Gaussian and Eisenstein integers Figure 2.5 shows some small norms in the Gaussian and Eisenstein domains. 
Figure 2.5. Norms in the Gaussian and Eisenstein domains Complex Multiplication Students of math are often confused when they first learn about complex numbers, because they are typically confronted with the counterintuitive concept of the square root of -1. This confusion is unnecessary if the goal is to gain a procedural understanding of the behaviors of complex numbers in the plane. In this book, i is not used at all. The only knowledge needed in this context is a basic understanding of complex addition and multiplication (and conjugation—a reflection about the real axis). Complex addition is accomplished by simply adding the real parts and the imaginary parts separately; it is the same as adding two vectors. Multiplication is key to understanding the magical powers of complex numbers. It is achieved through a particular “mixing” of the real and imaginary components of the factors to construct the real and imaginary parts of the product. Figure 2.6 shows how the integer (a,b) is multiplied by the integer (c,d) to create the real and imaginary parts of the resulting product. Complex multiplication can be thought of as a rotation and a dilation relative to the origin (an idea that will be revisited later). 
Figure 2.6. Complex multiplication 2. Root A “root” is defined here as an integer that is not a perfect power. It cannot be expressed in the form xn, where x has norm > 1 and where n is a rational integer > 1. The set of rational integers with this property is described in the On-line Encyclopedia of Integer Sequences at the web site: http://oeis.org/A007916 . This integer set is not given a name. So, for the present context, we will call it the set of “roots”. For illustration, consider the first 18 natural numbers: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 The roots are shown in bold-black, and the perfect powers are shown in light-gray. Note that the numbers 4, 8, and 16 are powers of the root 2, and 9 is a power of the root 3. Roots are primitive building blocks analogous to primes, except that instead of being primitives of multiplication, they are primitives of exponentiation. Let’s look at an example in the rational integers. The rational integer 125 is not a root: it is a perfect power, because it can be expressed in the form xn (53 = 125). Likewise, 25 is not a root: it is a perfect power, because it can be expressed in the form xn (52 = 25). But the number 5 is a root, since it has no integer roots of its own (other than itself, as 51). No integer multiplied by itself n times equals 5. All primes are roots, but not all roots are primes. For instance, the rational integer 10 is a root but it is not a prime: it is a root because no integer multiplied by itself n times equals 10. It is not a prime because 10 is the product of 2 and 5. The same definition can be applied to the complex integers: both domains have an infinite number of roots. They can be shown visually as a subset of points lying on the lattice. Three roots in each domain are shown—with norms—in Figure 2.7. In the Gaussian domain, they are (1,1), (2, 1), and (3, 0), having norms 2, 5, and 9. In the Eisenstein domain, they are (2, 1), (2, 0), and (3, 1), having norms 3, 4 and 7. 
Figure 2.7. Some roots (with norms shown) in the Gaussian and Eisenstein domains Units Figure 2.7 also shows the units (the dotted circles surrounding the origin). These have norm 1. Any rational integer multiplied by -1 keeps its magnitude and gets reflected to the opposite (positive or negative) side of the number line. Similarly, any complex integer multiplied by a unit will keep the same magnitude (and norm), and will optionally rotate about the origin. The units are not associated with any fractal curves; only the integers with norms greater than 1 have associated curves, and each integer represents a family of curves. This will become more clear when we consider the set of perfect powers that grow out of roots through exponentiation…which brings us to the concept of a family set. Family Set Power laws are important to fractals; they express self-similarity. The relationships among families of curves can also be described in terms of power laws. Consider the set of perfect powers of a root among the rational integers. For example, take the first five powers of the root 2: 21 = 2; 22 = 4; 23 = 8; 24 = 16; 25 = 32; A 2D analog of this series can be generated as the powers of the Gaussian integer (1,1), using complex number multiplication: (1,1)1 = (1,1); norm = 2 (1,1)2 = (0,2); norm = 4 (1,1)3 = (-2,2); norm = 8 (1,1)4 = (-4,0); norm = 16 (1,1)5 = (-4, -4); norm = 32 These Gaussian integers are plotted in Figure 2.8. The norms are labeled along the spiral. 
Figure 2.8. The G(1,1) family set lies on a power-of-2 spiral Starting from any root, we can generate a family set by calculating the consecutive integer powers of the root. Family sets are mutually disjoint, and the union of all family sets comprises the entire set of integers greater than norm 1. Using this categorization scheme ensures that all fractal curve families are taken into account. A family set can be referenced by its root. For instance, “the family set of E(2,1)” refers to E(2,1)n for all n > 0. Most family sets lie on logarithmic spirals, but some of them lie on straight lines (on the positive real axis), as shown in Figure 2.9. In this figure, four family sets are shown originating from roots with norms 2, 5, 9, and 10, shown in white circles. 
Figure 2.9. Four family sets in the Gaussian domain, showing norms The family sets in Figure 2.9 show the following norms (in bold-font) below. The roots are shown in the left column. 
So that all operations can be done within the gray slice, we will assume that any integers lying outside of the slice are mapped to it by way of reflections and rotations. As an example, Figure 2.10 shows how the G(1,1)n family set gets mapped into the gray slice, causing its associated power-of-two spiral to zigzag through the slice. 
Figure 2.10. The G(1,1)n family set remapped to the gray slice Primes Similar to a rational integer prime—which is only divisible by 1 and itself—a prime p in the Gaussian or Eisenstein domain is only divisible by a unit and one of its associates (that is: an integer with the same norm as p that is the product of p and a unit). The integer p cannot be written as the product of two integers that both have a smaller norm than p. Later we will take a look at some primes and their associated families. 3. Family A family is simply one of the integers existing in the family set. Every family set has an infinite number of families, starting at the root (the “root family”), and progressing through the family set (the “power families”). A family can be identified as a power of its root (e.g., E(2,1)3), with the exponent representing its order within the family set. Alternatively, it can be identified by its exact integer components (e.g., E(3,6)). In some cases, a family can be referenced simply by its norm, although multiple families can have the same norm. For example, the Eisenstein families E(3,1) and E(3,2) both have norm 7, as shown in Figure 2.11. They are reflections of each other (reflected about the line separating the gray slice from the one above it). (There are in fact 12 Eisenstein integers in all with norm 7, if you include all 12 slices of the plane). 
Figure 2.11. Two families with norm 7 There can also be families that have the same norm but they are not reflections of each other (such as G(3,4) and G(5,0), both having norm 25—these will be visited later). Tree Diagram The ranks described so far (domain, root, and family) are used to classify every family within the hierarchy. Each family is associated with a unique integer in the first (gray) slice of the complex plane. This hierarchical structure can also be visualized with a tree diagram (Figure 2.12). The trunk of the tree represents all plane-filling curves that can be generated using edge-replacement. The trunk splits off into two branches: the Gaussian domain and the Eisenstein domain. Each domain then splits off into an infinite number of branches representing the roots. A few of the smallest roots are shown, and the branch with the infinity symbol implies that there are infinitely more roots. Each root in turn branches off into its family set. There are infinitely many families in a family set, as indicated by the symbol rn. For each family shown, there is a representative curve at the end of the branch. Finally, the norm of the family is shown at the perimeter. 
Figure 2.12. A tree diagram illustrating the classification of curve families 4. Generator The last two ranks (generator and transform) specify the genetic code of each individual curve within a family. To understand a fractal curve generator, think of all the ways you can walk along a lattice. Consider the Eisenstein family at integer E(2,1), which is the dot labeled “3” we saw earlier in Figure 2.7. Its norm is 3. Figure 2.13 shows six paths starting from the origin (0,0)—denoted as A, and ending on the family integer E(2,1)—denoted as B, given exactly three unit steps. 
Figure 2.13. Six ways to walk a triangular lattice in three unit steps from A to B In the figure, the first two paths are framed with black boxes, indicating that they are unique. The other four paths can be described as isometric transformations of the first two. The number of steps (connected segments) in these paths is 3, which is the same as the family norm. Consider each path as a summation of three units in the Eisenstein domain. It demonstrates that there is more than one way to say “1+1+1” in the complex plane. This path is called the generator. The first two generators in Figure 2.13 can be represented as three integers in the Eisenstein domain: Generator 1: (1, 1), (0, -1), (1, 1) Generator 2: (1, 1), (1, 1), (0, -1) (Remember from Figure 2.3 that in the Eisenstein domain the specified integers are transformed (using ω) so that they conform to the triangular lattice). Fractal Generator as Array of Complex Integers Every fractal generator described in this book can be understood as an array of complex integers. And if the generator determines a plane-filling curve, then… the sum of these integers is equal to the family integer. Similarly, the sum of the norms of the integers is equal to the norm of the family integer. This can be expressed in a way that is related to the fractal (Hausdorff) dimension of a fractal curve. The equation D = log(N)/log(r) can be used to calculate the fractal dimension D of a curve, where N equals the number of segments in the fractal generator (assuming that each segment has length 1), and where r is the distance between the endpoints of the generator. A commonly-used example is the Koch curve, which has 4 segments of length 1 in its generator (N=4), and its generator spans a length of 3 (r=3). So for the Koch curve, D = log(4)/log(3) = 1.26186. Figure 2.14 shows the Koch curve along with three other curves of the E(3,0) family. It illustrates an exploration that is similar to one made previously by McKenna, who tested variations of the Koch curve in a triangular grid. Specifically, he was searching for curves confined to a triangle with sides of length 3, tiled with 9 sub-triangles [23]. 
Figure 2.14. Relatives of the Koch curve in the E(3,0) family For each curve, N and r are shown, along with the family norm f and fractal dimension D. In this taxonomy, the sum of the norms of the integers in the generator is equal to N, and the family norm f is equal to r2. Thus, for any plane-filling curve represented in this taxonomy… Mixed-Norm Generators, Divisors, and Power Laws The generators in Figure 2.14 each consist of integers that are units: their norms are all 1. An important point to introduce now is that many of the fascinating curves shown in this book are based on mixed-norm generators; their teragons have segments of varying lengths. These generators belong to the power families, which are all of the families in a family set except for the root family. Power families have curves with integers that can be either units or powers of the family root. This is related to the fact that fractal self-similarity obeys power laws. Consider a Gaussian integer with norm 4. There are four Gaussian integers that have a norm of 4: (2,0), (-2,0), (0,2), and (0,-2), shown as the white circles in Figure 2.15. The four roots of these integers: (1,1), (-1,1), (-1,-1), (1,-1) each have norm 2. Included are the four units: (1,0), (-1,0), (0,1), (0,-1). All the roots are shown as black dots. They have lines connecting them to the origin. It’s important to notice that the integers with norm 2 are connected with diagonal lines. 
Figure 2.15. Divisors (black dots) of Gaussian integers with norm 4 (white dots) How many ways can these integers be added up so that their sums equal a Gaussian integer with norm 4? (Let’s consider only one integer with norm 4—namely, (2,0)—since the other three are equal, except for the isometric transformations of rotation and reflection). One way to answer this question is with a picture: 
Figure 2.16. Ten ways to add Gaussian integers that sum to (2,0) In Figure 2.16, the four sums illustrated at the bottom have overlapping line segments, which make them appear to have only three segments. All fractal curve generators of a common family have integers that sum to the same integer (specifically, the family integer). But not any set of integers that sum to the family integer can be used as a generator that determines a plane-filling curve. For instance, consider a Gaussian integer of norm 5, such as G(2,1). It can be described as the sum of various permutations of Gaussian integers with norms 1, 2, and 4 (note that there is no such thing as a Gaussian integer with norm 3). Just a few of the many permutations are shown in Figure 2.17. 
Figure 2.17. A few permutations of integers with norms 1, 2, and 4 that sum to norm 5 None of these can be used as generators to make plane-filling curves. The reason is that Gaussian integers with norm 5 are prime; integers with norms 2 and 4 are not divisors of integers with norm 5. Only units are divisors in prime families. All of the integers in a generator must be divisors of the family integer. Furthermore, if the family integer is a perfect power, then those integers must be roots of the family integer. In terms of combinations of integer norms, all generators fall into the following categories: 1. root (the family integer is not a perfect power) a. prime (generator integers are units only) b. composite (generator integers may not all be units) 2. power (generator integers are roots of a power family integer) Prime families are root families whose generators only have integers of norm 1 (units). Generators of power families can have integers with a combination of norms (as long as they are all roots of the family integer). Note also that the divisors of power family integers are all powers of the family root; they are perfect powers. Primes, Composites, and Powers Figure 2.18, shows four generators with associated teragons. At the top-left is a generator of the prime family G(3,2) with norm 13 (all integers have norm 1). It was discovered in the process of developing this taxonomy—and described previously by McKenna [23]—it will be revisited later. At the top-right is a generator of the composite root family E(4,2) with norm 12 (all integers have norm 3, and they are all divisors of 12). At the bottom-left is a generator of the power family E(3,0) with norm 9 (the integers have norms 1 and 3). At the bottom-right is a generator of the power family E(4,0) with norm 16 (the integers have norms 1 and 4). It is the generator for the Tsunami Curve—illustrated at the beginning of the book. 
Figure 2.18. Generators with varying sized norms, with associated teragons Why must these generators only include divisors of the family integer? And why should generators with integers having varying norms only include integers that are powers of the family root? These rules may appear arbitrary at first, but the rationale should become clearer as we go. The fundamental principle at play here is that fractal self-similarity obeys power laws. What would happen if we attempted to break the rule by taking the upper-left generator and replacing the 4th and 5th integers with a single integer having norm 4? We know that 4 is not a divisor of 13, so we have a hint that there could be trouble ahead. This norm-4 integer is illustrated as the dark line in Figure 2.19a. Figure 2.19b shows how each integer is associated with a square area, shown as a gray square adjacent to the integer’s line segment. This association is indicated by a short line perpendicular to the line segment (this kind of association is explained later in the section on transforms). The large square associated with the norm 4 integer is shown in dark-gray. 
Figure 2.19. Experimental variation of the G(3,2) curve from Figure 2.18 We can see that overlapping areas and tremas (holes) begin to appear in the next two teragons, shown in (c) and (d). The same problem would occur if this larger square were oriented downward instead of upward. There appears to be no way to copy the generator onto this segment without causing a mess. With this taxonomy, the sum of the integers in a generator must be equal to the family integer. The experimental variation just described has a sum of 15. Notice that there is no such thing as a Gaussian integer with norm 15. (The norm of a Gaussian integer is always the sum of two squares). Both experimentation and number theory support the rationale for this rule. A similar experiment is shown in Figure 2.20. It is a variation of the Tsunami curve we just saw at the bottom-right of Figure 2.18. If we were to replace each of the three integers having norm 4 with two integers having norm 1, then we would end up with a total of 10 integers of norm 1, and the sum of the norms would go from 16 down to 10. Does there exist a plane-filling curve in the Eisenstein domain with norm 10? The gray triangles in Figure 2.20b may give a clue to the answer. The first four teragons of this curve are shown in Figure 2.20c with splined (curved) rendering. The result is interesting, but it is not plane-filling; the family integer has norm 16 but the sum of the generator’s integers has a norm of 10, so its fractal dimension is less than 2. 
Figure 2.20. Variation of the Tsunami curve from Figure 2.18 Emergent Morphology Now let’s return to the six generators shown at the top of Figure 2.16. These generators are responsible for the wonderful variety of shapes in Figure 2.21. 
Figure 2.21. The 6 generator shapes and 12 unique curves of the G(2,0) family How is it that such variety can emerge from these simple generators? The key lies in some special attributes that determine the transform—the final rank in the taxonomy. 5. Transform When explaining edge-replacement, we say that each segment in the generator is replaced with a small copy of the generator. (Fractal curve algorithms can use many methods to achieve the same effect). You could think of each copy as being transformed from the coordinate space of the generator to the coordinate space of the segment—which requires a translation, a rotation, and a scaling < 1. But there are additional transforms that can take place within the space of the segment. Imagine a strand of DNA that encodes for some aspect of a body plan being read backwards or upside-down. Let’s bring back our friend the Koch curve. Consider what happens if the instructions for drawing the Koch curve specified that the last segment be reflected so that it is upside-down. This can be illustrated with a turtle shown from the side-view (Figure 2.22). 
Figure 2.22. The Koch curve generator with its last segment reflected This reflection makes its influence on teragon 2, showing up as a downward bump in the last fourth of the curve (Figure 2.23). 
Figure 2.23. Second teragon of the Koch curve generator with its last segment reflected Notice how the reflection of the 16th segment has been re-reflected, putting the turtle upright again! This alternation of reflections continues each time the teragon is iterated. Figure 2.24. shows the result after iterating to teragon 4. 
Figure 2.24. Fourth teragon from Koch curve generator with its last segment reflected. Seeing the effect of a reflected segment in the Koch curve may not be very interesting. But it becomes more interesting (in fact, critical) when we see how transforming segments allows many plane-filling curves to be possible—and in particular, the self-avoiding ones. Consider the generator in Figure 2.25, which has no transforms. Teragons 1-6 are shown. 
Figure 2.25. A generator with no transforms that creates messy teragons Next, consider what happens if the second and fourth segments are reflected (Figure 2.26). 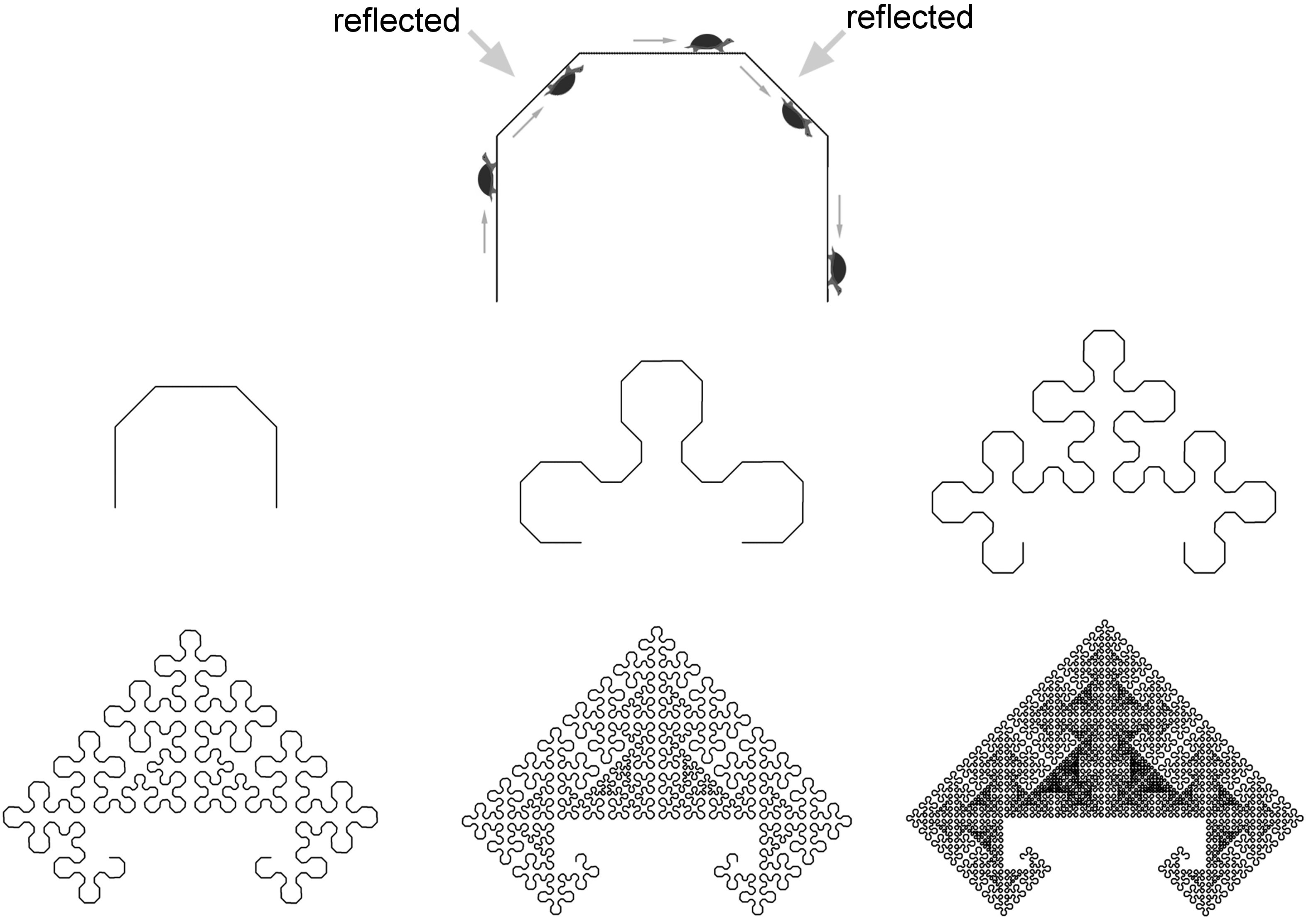
Figure 2.26. The same generator with alternating reflections By simply reflecting these two segments, the resulting curve avoids self-contact. Description of Transforms We have just seen the effect of reflecting segments. But the encoding for a transform on a segment actually has two components, which are both binary: rotation and reflection. The rotation component consists of a full 180-degree rotation about the center of the segment (for clarity, let’s call this a “180-rotation”). In the process of constructing transformed copies of the generator, a 180-rotation can be achieved by reading the generator’s integers and associated transforms backwards. A reflection can be achieved with two complex number operations: (1) taking the conjugate of the generator (its mirror-image on the opposite side of the real axis), and (2) assuming the family integer does not already lie on the real axis, multiplying the generator by the unit G(0,1) or E(0,1) to rotate it back to its axis of reflection. Figure 2.27 illustrates these operations as applied to the generator shown in Figure 2.26. (Although the generator is shown oriented upright in Figure 2.26, its natural pose is at a 45 degree angle, because it is in fact a member of the G(2,2) family). 
Figure 2.27. Two operations are used to reflect a generator about its family integer (Not all generators permit reflections, as explained later). Visualizing Transforms The chart in Figure 2.28 shows alternate visual representations for the four possible transforms, given all combinations of 180-rotations and reflections. These visual representations will be used in several illustrations throughout the book. 
Figure 2.28. Representations for transforms The generator for the Dragon of Eve is shown in Figure 2.29, demonstrating all four possible transforms. 
Figure 2.29. All possible transforms applied to the Dragon of Eve generator Note that a 180-rotation produces the same effect as two orthogonal reflections (one about the segment and one about a perpendicular that bisects the segment). This representation would work easily as well, and it is simpler in some ways, since all four transformations can be considered as combinations of these two reflections. In fact, this was used in a previous version of the taxonomy [35]. However, the 180-rotation operation has particular salience in the context of lattice symmetry, and it can be used on any generator segment, while the reflection operation only works for families that lie on an axis of reflection (as explained later in the section on axis-aligned curves). With this in mind, the representation was changed from two orthogonal reflections to a rotation plus a reflection. The Dragon of Eve generator can produce very different curves if alternate segments are 180-rotated. Figure 2.30 shows how 180-rotating the last segment of the generator determines the Dragon of Eve, while 180-rotating the middle segment creates a curve with intricate tiling patterns. 
Figure 2.30. The Dragon of Eve and a close relative Figure 2.31 shows an example a self-avoiding curve of the E(3,0) family that uses every combination of 180-rotations and reflections to stay out of its own way. 
Figure 2.31. A self-avoiding curve of the E(3,0) family with self-avoiding transforms The transforms for the segments of its generator are expressed as five pairs of bits: (1, 1), (1, 0), (0, 0), (0, 0), (0, 1). These transforms are illustrated with half arrows in the generator. The generator for the classic HH Dragon curve requires a (1, 0) transform in one of its two segments. Figure 2.32 shows a generator with the second segment 180-rotated, along with an associated teragon. 
Figure 2.32. HH Dragon generator and a high-order teragon The HH Dragon generator has only two segments. You may be wondering: what is the result of applying some other transforms on this 2-segment generator? Figure 2.33 shows three variations of transforms. 
Figure 2.33. Transforms for the Lévy C curve, the HH Dragon, and the Pólya curve When no transforms are used, the Lévy C curve results (left). This curve crosses and overlaps itself in a complicated way. The other two transforms result in two plane-filling curves (the only two in the G(1,1) family: the HH Dragon curve and the Pólya curve). But there are more transforms that can be applied to this generator. Figure 2.34 shows all 16 possible transforms. 
Figure 2.34. Curves resulting from every possible transform of the G(1,1) generator In this figure, two transforms determine the HH dragon; they are highlighted with squares in positions A2 and B1. Positions C4 and D3 show the two transforms that determine the Pólya curve. These curves are “well-behaved”, while the other curves either cross or overlap with themselves. The four curves in the middle are instances of the Cesàro Sweep (which has two variations, shown later in the G(1,1) and G(1,1)2 families). Now let’s return to the first two paths shown in Figure 2.13. They represent the generators of the E(2,1) family, with norm 3. Given all possible permutations of transforms, how many admit plane-filling curves? The answer is 10 (Figure 2.35). 
Figure 2.35. The 10 curves of the E(2,1) family, shown with generators Curve (a) is the Terdragon. It has no transforms. Curve (b) is the result of reflecting all 3 segments of the Terdragon. Curve (d) is the “Fractal Chair” [4]. Curve (e) is the “Half-Terdragon” [20]. Curve (j) is the “Walking Terdragon” [36]. Curves (h) and (j) are both self-avoiding. Curve (c) is the result of reflecting the first and third segments of the Terdragon (Figure 2.36, lower-right). Note that the first and third segments have been reflected in the Terdragon generator to determine this curve. These reflections are shown with dark lines in the middle of the figure. Haverkort [16] made the observation that this curve is basically a stretched version of the original Peano curve [25]. 
Figure 2.36. Ter Dragon and a transformed version similar to the original Peano curve What would happen if 180-rotations had been used instead of reflections? The answer is…nothing, because this generator has point-symmetry about its center: it is identical to itself when rotated 180-degrees. The symmetry of a generator determines how it can be transformed in the lattice. For instance, consider the generator for the 5-Dragon (Figure 2.37). Like the Terdragon generator, it has point-symmetry, and so a 180-rotation has no effect. But unlike the Terdragon generator, it cannot be reflected, because that would break it out of the lattice, as shown at bottom-right. 
Figure 2.37. 5-Dragon generator demonstrates how G(2,1) curves do not allow reflections This point will be revisited later when we explore a variation of the 5-Dragon in the G(5,0) family. Transforming segments appears to be a necessary ingredient for generating self-avoiding curves, as exemplified by the two curves in Figure 2.38. (Notice how different transforms are applied to the same generator, resulting in subtle differences in their teragons). 
Figure 2.38. Curves of the E(3,0) family: same generator but different transforms Summary Now that all five ranks of the taxonomy have been described, let’s see how a particular curve—the Dragon of Eve—fits into this hierarchy. In Figure 2.39, the family G(1,1)2 = G(0,2) has four unique generators that admit plane-filling curves. For sake of illustration, they are rotated by 90 degrees, as if they belonged to the G(2,0) family. 
Figure 2.39. An illustration of how the Dragon of Eve fits in the taxonomic hierarchy 
Figure 2.40. A curve of the E(3,1) family (splined) |